
はじめに
以前の研究員の眼「 人間の直感の不確実性-数学的な正しさと乖離している場合があることを知っていますか- 」で、「誕生日のパラドックス」について紹介したところ、複数の照会があり、いくつかの質問を受けた。今回は、いろいろなケースで「誕生日が一致する確率」について、どのようになるのか紹介したい。
具体的には、(1)「(少なくとも2人1組ではなくて)2組以上のペアの誕生日が一致している確率」はどうなるのか、(2)「3人以上の誕生日が一致している確率」はどうなるのか、という問題である。
これからの年末年始の時期等に、多くの人が集まる場で話題にでもしてもらえればと思って、このトピックを採り上げることにした。
問題の設定
ある部屋に50人のグループがいると仮定する。以下のように、いろいろなケースで誕生日が一致する確率を考えてみる(なお、今回の計算では、1年365日とした)。
問題(その1)
まずは、個人を特定せずに、グループ全体での発生確率の問題を考える。
問題1 部屋の中の全員の誕生日が異なる確率 P0
問題2 (部屋の中の誰でもよいので)最低1組2人のペアの誕生日が一致している確率 Q1
(ここでは、3人以上の誕生日が一致している場合は、含まれないとする。以下、同様)
(※) これに対して、少なくとも誰かと誰かの誕生日が一致する確率 R1(=1-P0)も考えられる。この場合には、3人以上の誕生日が一致している場合も含まれる。以前の「研究員の眼」で述べたのは、このケースであり、この確率が人間の直感に比べて予想外に高いことが「誕生日のパラドックス」と呼ばれる由縁となっている。
問題3 丁度1組2人のペアの誕生日が一致している確率 P1
問題4 最低2組のペアの誕生日が一致している確率 Q2
問題5 丁度2組4人のペアの誕生日が一致している確率 P2
問題6 最低3組のペアの誕生日が一致している確率 Q3
問題7 丁度3組のペアの誕生日が一致している確率 P3
以下、同様に、丁度k組の2人ずつのペアの誕生日が一致している確率Pkや最低k組のペアの誕生日が一致している確率Qkが考えられる。この場合、
Qk=P1+P2+ ・・・・・ + Pk、あるいは、Pk = Qk-Q(k-1)
となる。
問題(その1)の解答
例えば、問題7を考えると、6人(2人×3組)が3種類の誕生日で、44人は残りの362日の全て異なる誕生日となるので、そのような誕生日が発生するパターンの数は、

となる。よって、求める確率は、これを全ての発生パターンの「365の50乗」で割ることによって、
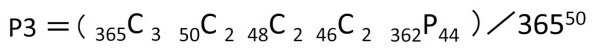
で、結果として P3=22.2% となる。
以上の考え方に基づいて計算した結果をまとめると、次表の通りとなる。
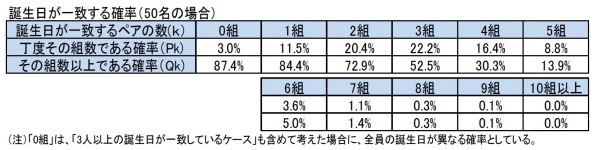
これによると、50人のグループでは、以下の状況になっている。
(1)全員の誕生日が異なる確率は「0組」の数の3.0%であることから、少なくとも誰かと誰かの誕生日が一致している確率は97.0%となる。
(2)誕生日が一致するペアの数としては、「3組」が最も多い。
(3)さすがに7組以上のペアが発生する確率は1.4%と低くなるが、それでも5組のペアが発生する確率は8.8%もあり、6組のペアが発生する確率も3.6%ある。
(4)一方で、全く誕生日が一致しないか、1組2人のペアの誕生日しか一致しない確率は、わずか14.5%(3.0%+11.5%)でしかない。このことはまた、誕生日が他の人と一致している人が3人以上(1組でも3人以上又は2組以上)いる確率は、85.5%ということになる。
(5)2組以上のペアが発生する確率は72.9%、3組以上のペアが発生する確率は52.5%となる。
(6)上記の表の0組以上の発生確率が87.4%となっているが、これと100%との差異の12.6%は、今回の計算で考慮されていない、「少なくとも3人以上の誕生日が一致している組が1つは存在している確率」となる。
(7)即ち、例えば、上記の表の「3組」には、「1組が3人の誕生日が一致、2組(あるいは3組)が2人の誕生日が一致」しているケース等は含まれていない。こうしたケースを含めれば、上記の表の確率はさらに高くなることになる。
(8)因みに、上記の表に基づくと、誕生日が一致するペアの数の期待値は、2.6組ということになる。50人いれば、平均して2.6組のペアの誕生日が一致していることになる。(7)で述べた3人以上の誕生日が一致しているケースも含めれば、さらに高い期待値になる。
50人のグループで考えても、例えば誕生日が一致しているペアが5組あることも決して珍しくない、ということになる。
なお、上に述べたように、「少なくとも3人以上の誕生日が一致している組が1つは存在している確率」は12.6%であるが、これが「少なくとも4人以上の誕生日が一致している組が1つは存在している確率」となると1%未満でぐっと小さくなる。一定数の組のペアが一致しているケースに比べて、一定人数の誕生日が一致するケースは、より発生が限られている。