問題(その2)
次に、特定の個人に関しての発生確率を考える。
問題 8 自分と同じ誕生日の人がいない確率 S0
問題 9 自分と誰かの誕生日が一致している確率
(自分と同じ誕生日の人が他に1人以上いる確率)T1(=1-S0)
問題10 自分と同じ誕生日の人が他に丁度1人いる確率 S1
問題11 自分と同じ誕生日の人が他に2人以上いる確率 T2
問題12 自分と同じ誕生日の人が他に丁度2人いる確率 S2
問題13 自分と同じ誕生日の人が他に3人以上いる確率 T3
問題14 自分と同じ誕生日の人が他に丁度3人いる確率 S3
以下、同様に、自分と同じ誕生日の人が丁度k人いる確率Skや自分と同じ誕生日の人が最低k人いる確率Tkが考えられる。この場合、
Tk=S1+S2+ ・・・・・ + Sk、あるいは、Sk = Tk-T(k-1)
となる。
問題(その2)の解答
例えば、自分と同じ誕生日の人が他に丁度2人いるということは、2人が自分と同じ誕生日(その確率はそれぞれ1/365)で、それ以外の47人は自分とは異なる誕生日(その確率はそれぞれ364/365)であり、自分以外の49人からの2人の組合せは 49C2 通りあるので、
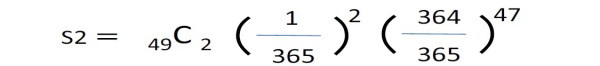
で、結果として S2=0.8% となる。
以上をまとめると、以下の表の通りとなる。

こちらの確率は、さすがに低いものとなる。
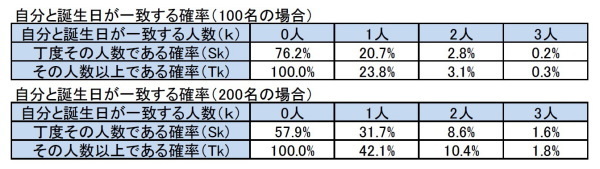
なお、人数が100名及び200名の場合には、以下の通りとなり、自分と同じ誕生日の人がいる確率はそれぞれ23.8%、42.1%と高くなっていく。さらには、自分と同じ誕生日の人が2人以上いる確率もそれぞれ3.1%、10.4%と高くなっていく。
まとめ
以前の 研究員の眼 と同様に、今回の結果についても驚かれた方が多いのではないかと思われる。
ここでは誕生日をテーマにしているが、一般的に人間は、何かの事象の発生確率を想定する場合に、無意識的に自分を中心に起こるケースを想定して、その発生確率は低いものだと想定しているのではないか。ところが、グループ全体として考える場合には、個人が想定しているよりもかなり高い確率でその事象が発生することになる。
このことは、物事を考えていく場合に何か示唆するものがあるのではないかと思われる。
順列・組み合わせの問題については、中学・高校時代にかなり苦労された方も多いのではないかと思う。しかし、こうやって考えてみると、その解答を導き出すのは必ずしも易しくないとしても、その結果には感動させられることもあるのではないかと思われる。これを機に、今一度若い頃に戻って、いろいろな順列・組み合わせが関係してくる確率の問題を考えてみるのも、頭の体操になってよいのではないか。
中村亮一(なかむら りょういち)
ニッセイ基礎研究所 保険研究部
取締役
【関連記事】
・
人間の直感の不確実性-数学的な正しさと乖離している場合があることを知っていますか-
・
出会い(マッチング)の確率-世の中の各種事象において、出会い(マッチング)が起こる確率は、結構高いってこと知っていますか-
・
世の中の数字の現われ方は一律ではないって知っていましたか―ベンフォードの法則について―
・
自動運転の普及と津波避難対策-完全自動運転が普及した社会を想像する。その1
・
GDP統計の改定で1%近くまで高まった日本の潜在成長率-ゼロ%台前半を前提にした悲観論は間違いだった?