正しい使い方ができてる人は案外多くない
日本人は「確率や統計が好きな国民」と言われています。広告はもちろん、タイトル勝負のメディアでも「婚活成功組に聞いた『勝率9割アップのメイク術!』」「【悲報】ハゲの遺伝率は▲▲%」など、人目を引けるように確率を混ぜた表現が多く見られます。
一方で「確率や統計に関する正しい考え方」が根付いているとは言いがたい現状があります。たとえば、将棋やスポーツなどの勝率について「勝つか負けるかの50%」で考える人もいますが、勝負事には実力差など多数の因子が影響するため、コイントスのように考えるのは現実的ではありません。
そこで「確率に関する正しい考え方の基礎」を学び、生活に密着した使い方をみてみましょう。
確率とは一体何か
ほとんどの人は、確率について小中学校で次のように習っていると思います。
しかし、ここでいくつか注意しなければならない点があります。たとえば、正しく作られたサイコロを6回振って、たまたま2が一回もでなかったとします。それを受けて「サイコロを振って2が出る確率は0である」と言う人がいたら、さすがにおかしいと思う人も多いでしょう。
このように試行回数が少ないと結果のばらつきが大きく、確率とはみなせない値になりますが、これを100回、1000回、1万回……と繰り返していくとm/nがほぼ一定の値に収れんしていきます。こうして定まったm/nの値を 統計的確率 と呼びます。
一方、計算によって求めた確率を
理論的確率
(もしくは数学的確率)と言います。上記の例で言えば「2の目が出る確率は1/6≒0.167(約16.7%)」と計算で求めた値がそうです。
ガチャと天気と理論的確率
理論的確率は、一部の結果から全体を推測する「 推測統計学 (あるいは推計統計学)」でよく用いられています。たとえば、天気予報では「今日午前の降水確率は30%」などと確率を用いて表現されますが、実際に同じ天気を何度も繰り返して試すことはできません。
この場合、過去の似たような天気や大気の状態、雲の配置、風向きなど、多数の要素から算出し「今日の午前のような天気が仮に100回あったとしたら、そのうち30回は雨だろう」という意味で「降水確率30%」と表現しています。
その他、身近な理論的確率の使い方として「ソシャゲ(ソーシャルゲーム)のガチャにおける、アイテムの出現確率」があります。まず、アイテムの出現方式が統計学でいうところの 復元抽出方式 か 非復元抽出方式 かで計算が異なるため、そこから整理します。
一般的にイメージしやすいのは、非復元抽出方式のガチャでしょう。現実のガチャガチャがまわすたびに中のカプセル数が減っていくように、最初に定められた抽選対象がガチャをまわすたびに減っていくもので、「ボックスガチャ」などと通称されています。
例として、抽選対象が100あるなかから出現率1%のアイテムを狙う場合を考えてみましょう。初回でとれる確率は1%とそのままですが、2回目は1/99≒1.01%、10回目で1/90≒1.11%……と入手確率が上昇し、どんなに運が悪くても100回まわせば確実にゲットできる計算になります。
しかし、 復元抽出方式のガチャの場合は事情が異なります 。初回もそれ以後も、母集団である抽選対象の数は変わりません。上の「100の抽選対象から出現率1%のアイテムを狙う」と同じ条件で、ガチャを100回まわすまでにアイテムを取れる確率を計算してみましょう。
100回目までにゲットできる確率は「全体から、100回連続で外し続ける確率を引く」ことで算出 できます。この場合、外れる確率は99%なので、1から0.99の100乗を引いた数、約0.639(≒64%)が求める値となります。
逆に言えば「100回まわしてもゲットできない確率は約36%」ということなので、100人がこのガチャをまわしたとすると、36人は目当てのアイテムが取れないことになります(ちなみに200回だと約14%、300回でも約5%の人が取れない計算になります)。
ガチャの例のように、同じ1%を狙う場合でも結果が大きく異なることがあるように、確率の世界は奥が深く、身近なところで役に立つものです。興味がわいてきた方は、計算や数字を毛嫌いせずに学んでみてはいかがでしょうか。
(提供: 日本実業出版社 )
【編集部のオススメ
日本実業出版社記事
】
・
選挙速報で開票率1%なのに当確が出るしくみ
・
ありきたりの問題に飽きた人に贈る数学<超絶>難問集
・
データ分析手法をたくさん知ってたってムダなだけ
・
“論理的な間違い”はこうして生まれる ―ロジカル・シンキングの落とし穴
・
数学はこんなに働いている【著者からのメッセージ】
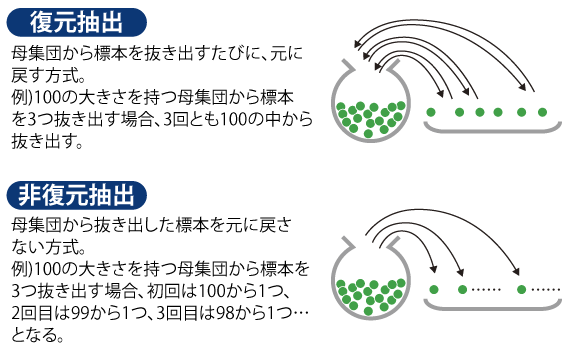 抽出方法の違い(『
抽出方法の違い(『