本記事は、澤上 龍氏の著書『長期投資家の思考法 資産を増やし、社会を豊かにする』(明日香出版社)の中から一部を抜粋・編集しています。

複利はまやかしで単なる宣伝文句だった
資産運用は時間を味方にするべきとしばしば言われる。背景に複利効果があるからだ。複利はとんでもない発明だと言ったのはアインシュタイン氏だったか…… ともあれ「長期で資産を増やすためには複利効果」は誰もが使う合言葉だ。
しかし実際、資産運用の世界で複利は概念上の存在でしかない。なぜなら複利利回りを確約する商品がないから。あるとすれば「仮に7%で回ったら10年で2倍になる計算」との言い回しだけ。
計算上は確かにそうだが、それはシミュレーションの世界。実在する複利は借金の利息だけで、利回りも契約で確定しているため間違いない……あれが雪ダルマ式に増える恐ろしさと言ったら半端ではない。
さて、そんなイメージ先行の宣伝文句をどうしてあらゆる金融機関が使うのか。詐欺であればとっくに行政指導が入るか逮捕されているはず。しかしそうならないのは、概念としてのみ説明するからなのだろう。
実際の金融商品において運用成績を複利利回りで表記するものがある。あれらは結果からの逆算、つまり「これまでの実績を複利年率に置き換えると」というまやかしだ。もちろん未来に対しての約束はできない。
複利はないが「複利効果」はある。いや、複利っぽい考え方と言うべきか。金融機関の「複利なので」という嘘を内部告発的に一蹴しつつ、資産運用や企業経営における本当の複利効果を考えていきたい。
そもそも複利とは何か
雪玉を転がすたびに表面積が大きくなり、付着する雪も増えて玉の巨大化が加速する…… 複利とはそんなイメージだ。
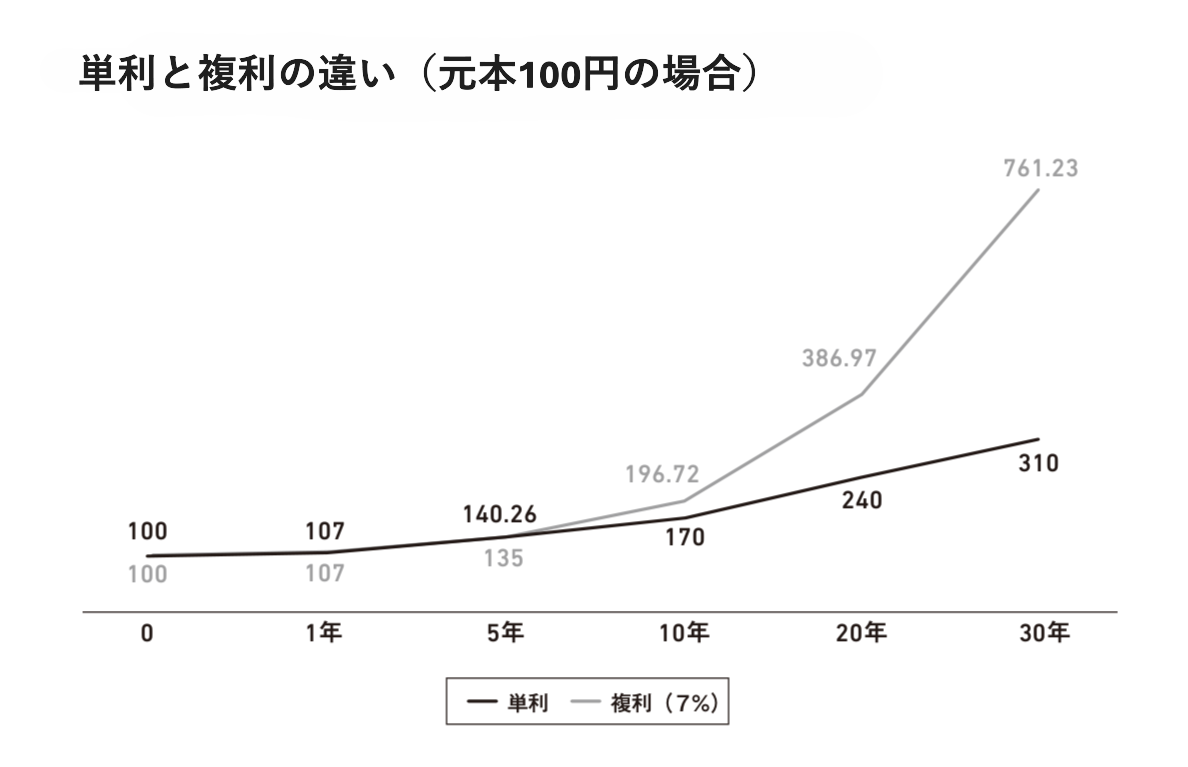
毎年7%の単利と複利を比べてみよう。100円を元金にした単利では、1年後に107円、2年後に114円、3年後は121円……と毎年7円(100円の7%)ずつ増えていく。10年後には170円(100円+7円×10年)、20年後には240円(100円+7円×20年)、そして30年後には310円に到達する(100円+7円×30年)。
他方で複利は元金と利息が土台となるので、1年後に107円、2年後には114.49円、3年後には122.50円となり、10年後は約2倍の196.72円、20年後にはその倍の386.97円、そしてなんと30年後にはさらにその倍の761.23円まで膨らむのだ。
単利の直線的な伸びに対し、複利は指数関数的な伸びを示す。皆が複利を使えと言いたくなる気持ちも分かる…… まやかしだが。
種銭の大きさと転がせる時間の長さが大事
さて、もう少し実践的な数字で試してみよう。
若年~青年世代には時間はあるがお金がない。壮年~中年世代には時間は限られるが積み上げたお金がある。たとえば25歳のA氏が初回の投資100万円のみをゴールである65歳まで運用する。
他方で45歳のB氏は65歳のゴールまで20年しかないが、手元には385万円ある。利回りは年率平均7%だとすると、A・B氏共に老後に約1,500万円を手に入れることが可能となる。この計算では、A氏の100万円は20年後のB氏の年齢になるときに約385万円まで膨らんでいることと同じだ。
老後に1,500万円では不足すると考えるならば、A・B氏共に年齢を重ねながらもつみたて投資を実行すればよい。
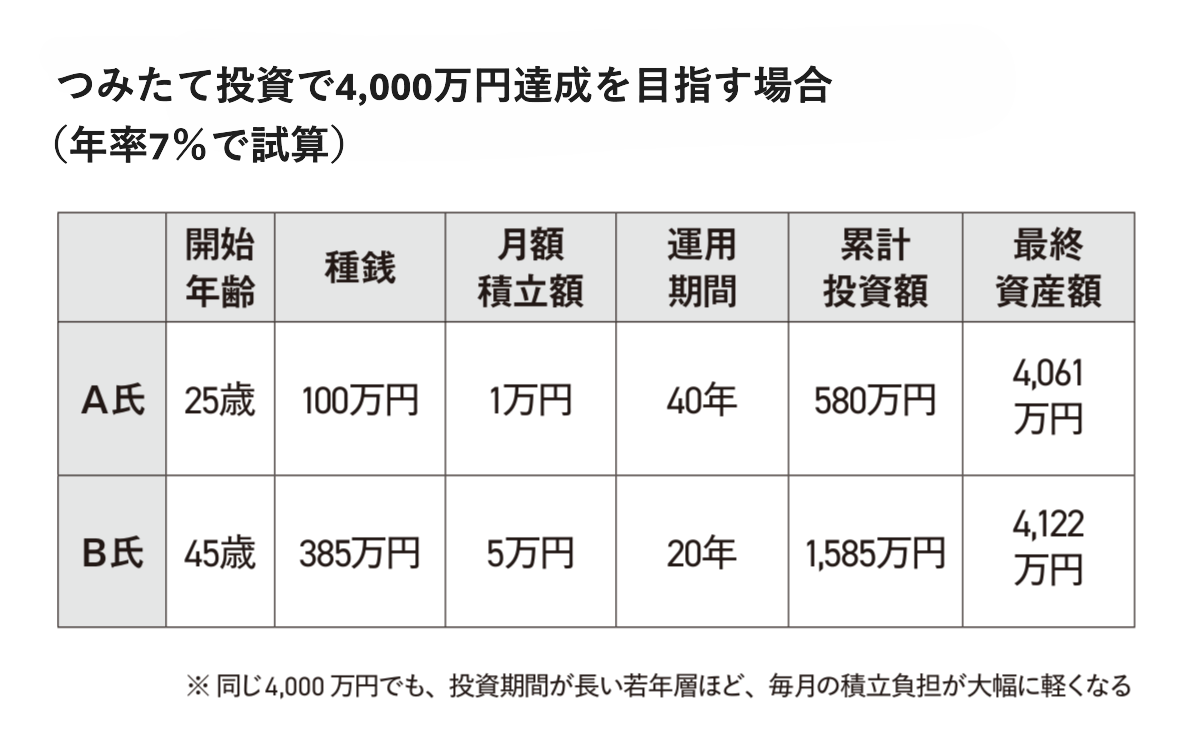
ゴールの65歳で4,000万円を手にしたいなら、A氏であれば1万円、B氏であれば5万円弱を毎月投資すれば叶うだろう。簡易計算だがイメージは伝わるはずだ。
なお、つみたて投資の累計額はA氏480万円、B氏1,160万円となる。
以上の計算から、資産運用における複利効果を最大化するなら「なるべく早く玉の表面積を大きくすること」に尽きると分かる。
利回りが一定だと仮定すれば、最大化の鍵は種銭(初期投資の額)の大きさと転がせる時間の長さとなるのだ。あくまでもシミュレーションだが。
まやかしである複利を壊す方法は簡単。途中で引き出すことだ。
表面積を加速度的に大きくしていくのが複利効果であるため、途中で雪玉の雪を削り落としたら効果が激減するのはすぐに理解できるだろう。だから買ったり売ったりするよりも、長く運用したほうがいいとの説明につながる。
また商品設計上で複利効果を破棄しているのが毎月分配型ファンドだ。毎月削るって…… そもそも増やす気などないのだ。

※画像をクリックするとAmazonに飛びます。
