本記事は、田渕 直也氏の著書『金融と投資のための確率・統計の基本』(日本実業出版社)の中から一部を抜粋・編集しています。

期待リターンとは?
何かに投資するときに、最初の出発点となるべきは「どのくらい儲かりそうか」ということでしょう。それが、最初に取り上げるテーマ、期待リターンです。ちなみに、リターンは収益率という意味の言葉です。
気をつけなければいけない点は、期待リターンの「期待」が個人的な希望を意味しているわけではないということです。
この「期待」という言葉は、確率論の用語である期待値からきているもので、将来に発生する未確定の何らかの値に対して、現時点で合理的、客観的に見積もることができる平均的な予測値を示します。同じ意味を表すのに、たんに平均という言葉が使われる場合もあります。
たとえば株式に投資することを考えたとして、自分の勝手な思い込みや一方的な希望を排して、平均的にみてだいたいどのくらい儲かりそうかを合理的、客観的に見積もったものが株式投資の期待リターンということになります。
何かをするときに、その結果がどうなりそうかを考えてから行動するのは、ある意味で当然のことですね。ところが、ひとつ重大な問題があって、期待リターンの正確な値は誰にもわからないのです。したがって、何らかの方法で推定しなければなりませんが、いったいどのような方法が考えられるでしょうか。
まず考えられるのは、「過去に起きたことはこれからも繰り返される」と考えて、過去の収益率を調べてみることです。
もっとも、この考え方だと過去に例をみない出来事が起きることを予見できないわけですから、将来の予測方法として完全ではありません。
それでは、過去にとらわれずに将来起きるかもしれないことをあれこれ考えていかなければいけないのかというと、もちろんそうしたシナリオづくりはとても大切なことですが、根拠にもとづかないシナリオづくりはどうしても客観性を欠いてしまいます。したがって、たとえ過去にとらわれない将来のシナリオづくりを目指すとしても、まずは過去を分析することから始めることが得策でしょう。
過去の収益率は期待リターンを表すのか
~母平均の推定と大数の法則
例として日経平均株価※1を考えます。日経平均株価にできるだけ連動するような投資をした場合、1年あたりの期待リターンはどのくらいになるでしょうか。
ちなみに、株式の投資リターンには、株価の変動による損益と配当による収益があります。その2つを合わせたものが株式投資のトータルリターンと呼ばれるものですが、ここでは配当を無視して価格変動による損益のみを考えます。なお、リターンはもともと収益を意味する言葉ですが、株価変動は損失に結びつく場合もあり、その場合はマイナスのリターンということになります。
さて2023年1年間で、日経平均株価は28.2%上昇しました。この上昇率がこれからも毎年続くと考えて、これを期待リターンと捉えてもいいのでしょうか。
株価の変動は、毎年その率が異なっています。もちろん株価が下落することだってあります。実際、2023年のプラス28.2%という数字は、それまでの10年間で最高の数字です。
※1 日本の代表的な上場企業225社の株価の平均から算出されるものです。あとで出てくる東証株価指数(TOPIX)とともに、日本の株式市場の動向を端的に表す指数としてよく用いられています。
そんな数字を、未来永劫に毎年繰り返されていくものと捉えるのはさすがに無理がありますね。
それでは、2014年から2023年まで10年間の年間変動率を調べて、その平均を取ればどうでしょうか。各年の株価変動率にはバラツキがあって、単年の変動率が将来の変動率の最適な予測値にはなりそうにないことがわかります。一方、10年間の平均変動率はプラス8.2%となっていて、各年の変動率はその値を中心に上下に振れているように見えます。これを期待リターンの近似値とみなすことは、それほど無茶ではない気がします。
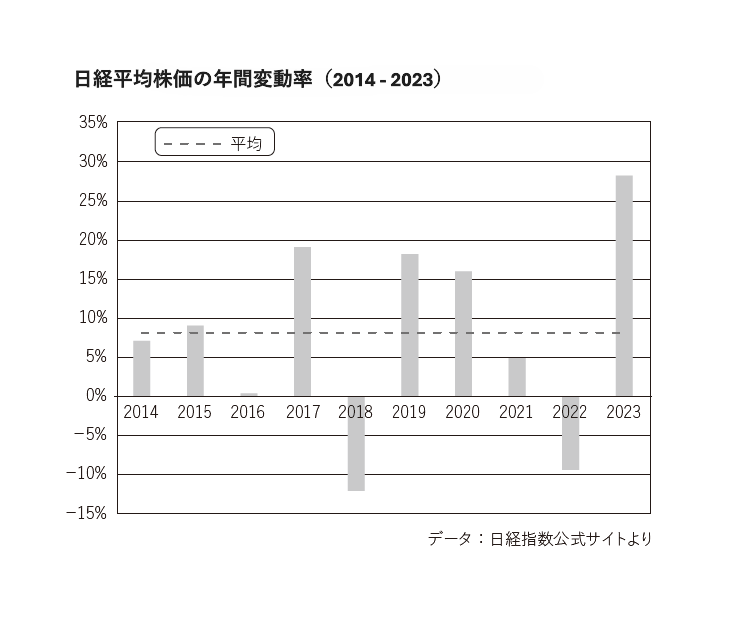
ですが、参照する期間は10年でいいのでしょうか。試しに、もっと過去にまで遡ってみましょう。1949年以来の年間変動率※2の平均は、10.4%です。どの数字が期待リターンの推定値として最も適切でしょうか。
※2 1949年のみ、その年の始値から終値の変化率、それ以外は前年終値から当年の終値の変化率を使っています。

ここで、次のようなことをイメージしてみましょう。
日経平均株価の年間変動率には、あらかじめ取り得る値が決まっているとします。その全体をわれわれが知ることはできませんが、無数の取り得る変動率の値が書かれた札が箱に入っていて、毎年神様がそのなかから札を1つだけ取り出します。そして、その年に選ばれた札どおりに株価が変動すると考えます。
ここで少々、用語の解説をすると、株価の変動率のように、ある一定の確率に従って様々な値を取るものを確率変数と呼びます。そして、その確率変数が取り得るすべての値が含まれた集合、つまりこの場合だと、あり得る株価変動率の値が書かれたすべての札を含む箱の中身全体を、母集団と呼びます。
いまここで求めようとしている期待リターンは、この母集団の平均、すなわち母平均と呼ばれるものに他なりません。ですが、母集団の全体像は誰も知らないので、これを推定していかなければならないのです。
ここでは、過去、実際に実現した年間変動率を、神様が母集団から選び出したサンプルデータとして考えています。このサンプルデータをいくつか集めたものを標本(サンプル)といいますが、標本には、そこに含まれるサンプルデータの数によって様々なサイズのものが考えられます。①はサンプル数1の標本、②はサンプル数10の標本、そして③はサンプル数75の標本です。これら標本ごとの平均を計算したものが標本平均です。
さて、母集団が時間経過に伴って変化してしまうようなものではなく、かつ各サンプルデータも毎回完全にランダムに選ばれているとすると、標本平均は、標本サイズを多くしていくことによって次第に母平均から乖離する可能性が低くなるはずだと考えることができるでしょう。原理的には、標本サイズを無限大にまで拡大できれば、母集団の値がまんべんなく選ばれて、標本平均が母平均に近づいていくことが予想されるからです。これが、確率統計論で最も基本的な定理のひとつである大数の法則です。
つまり、大数の法則が成り立つならば、できるだけ多くのサンプルデータから平均を取ることで、より適切な母平均の推定ができることになります。
株価変動率についてもこの大数の法則が適用可能だとすると、日経平均株価の期待リターンの推定値は、最も標本サイズが大きい③の標本平均10.4%が最も適切である可能性が高いということになるでしょう。

※画像をクリックするとAmazonに飛びます。
- 28.2%の幻想と10.4%の現実、株式投資における期待リターンの捉え方
- ボラティリティとは何か? 期待リターンの裏に潜むもう1つの真実
- なぜ確率は「山の形」になるのか? 正規分布と中心極限定理
- ひとつのかごに卵を入れない、分散投資の知恵
- 株価はなぜ動く? 市場モデルで解き明かす「リスク」の正体
- 「VaR」が金融を変えた! リスク管理の常識を覆した革命とは
- 「過去は未来を保証しない」ブラック・スワンに備える思考法
