本記事は、田渕 直也氏の著書『金融と投資のための確率・統計の基本』(日本実業出版社)の中から一部を抜粋・編集しています。

ランダムな動きが続くと現れる正規分布
~中心極限定理
金融実務では至る所で正規分布を仮定した確率計算が行なわれています。まずは、この正規分布がいかなるものかというところから見ていきましょう。
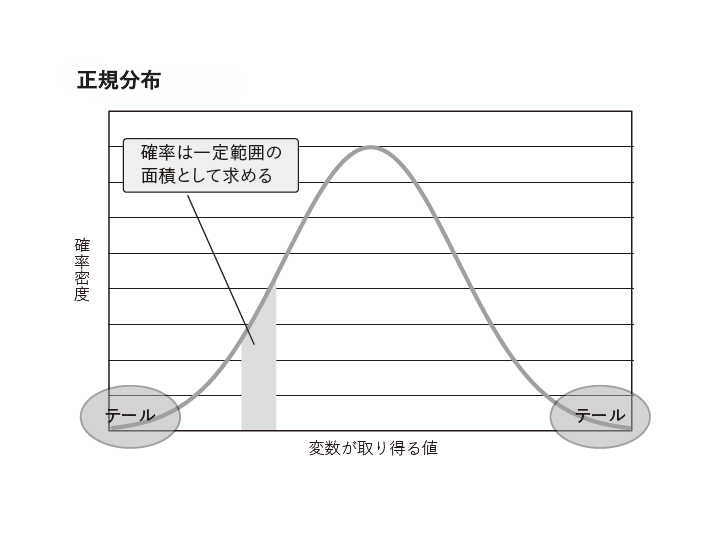
正規分布は、図のような形をした確率分布です。何回かサイコロを振って平均を取ることを繰り返していったときの平均値の確率分布は、平均を計算するためにサイコロを振る回数をどんどん増やしていくと、正規分布に近づいていくことが知られています。
このサイコロを振る回数をさらに増やすと、さらに正規分布に近づいていくのです。
サイコロの目が出る確率は、もともとは一様分布といわれる横一線の確率分布でした。ですが、それを何回も積み重ねた結果はなぜか正規分布になっているというわけです。
コイン投げでも一緒です。コイン投げは1回の試行で表か裏のどちらかの結果が出ます。確率は2分の1ずつと考えていいでしょう。これも一様分布ですね。これを何回か行なって、表が出ればプラス1点、裏が出ればマイナス1点として、合計値を求めます。コインを投げる回数を増やしていくと、やはりその合計値の確率分布は正規分布に近づいていきます。合計値をコイン投げの回数で割った平均値でももちろん同じことです。
つまり、元の確率分布が正規分布ではないものでも、ランダムな試行を積み重ねていった結果の和や平均といった値の分布は、試行回数を増やすにつれて正規分布に近づいていくのです。これが、「中心極限定理」と呼ばれる確率統計論の重要定理です。
中心極限定理は、厳密にいうと2つの内容からなり、「(どんなものであれ)母集団からランダムに抽出した標本の平均の分布は、標本のサイズを大きくすると正規分布に近づく」ことに加え、「標本のサイズを大きくすればするほど、その正規分布の標準偏差が小さくなっていく」というものです。
大数の法則と似ていますが、少し視点が異なります。大数の法則は、標本のサイズを大きくすることで標本平均が母平均に近づいていくことを表現しているのに対して、中心極限定理は、標本平均と母平均のずれに焦点を当て、そのずれの分布が正規分布に近づき、かつ次第にその標準偏差が小さくなることを表しています。
1日の株価変動は、神様が瞬間ごとの株価変動率の母集団からランダムに引いた値の累積効果によって実現するものですから、要するに十分に大きなサイズの標本の合計値によって決まると考えることができます。そうであれば、中心極限定理により1日あたりの株価変動率は正規分布に近い形になるはずです。
ということは、1年あたりの株価変動率は1年というさらに大きな標本の積み重ねであり、その分布は正規分布により近づいていくはずです。
このように、母集団がどんなものであっても※1、大きなサイズの標本平均と考えられるものを扱う場合は正規分布として扱ってもよい、という中心極限定理によって、正規分布は確率統計論において特別な存在意義を持つものとなっているのです。
※1 厳密にいえば、中心極限定理には、大数の法則と同様、独立同一分布というものが仮定されています。また、実際の値がわからないとしても、原理的に母平均や母分散が存在することが必要です。
ただし、中心極限定理が働くためには、ランダムな試行の積み重ねが必要です。たとえば前章で見た身長の分布は、正規分布に非常に近い形をしています。このようなものは他にも様々にあるのですが、なぜ身長は正規分布に従うのでしょうか。それは、身長の差が、おそらくは遺伝的な変異などランダムな要因の積み重ねによって大きな影響を受けているであろうことを反映しています。
ランダムな動きの積み重ねは正規分布を導き、逆に正規分布にはその背後にランダムな動きの積み重ねがあるということです。
正規分布の特徴
正規分布にはいくつもの特徴があります。
まず、正規分布は連続型の確率分布です。たとえばサイコロを振る場合、出る目は1から6までの6つの値しかありません。このように、確率変数の値が飛び飛びになっている場合の確率分布を離散型確率分布と呼びます。
次に、サイコロを複数回振って平均を取ることを考え、(現実には無理ですが)試行回数を無限大にすると、平均値はどんなに細かい値も取れるようになり、飛び飛びがなくなって1本のなめらかな線で確率分布を表現できるようになります。それが連続型確率分布です。
連続型確率分布では、特定の値を取る確率が何%かということは計算できません。他に取り得る値が無数にあるからです。したがって、図の縦軸で示される確率の大きさは、何%という一般的な確率ではなく、確率密度と呼ばれるものになります。もっとも確率密度は、何%という形で表されるものではないとしても、確率の大きさを表すものであることには違いありません。
この確率密度から一般的な何%という形の確率を計算するためには、確率変数の範囲を特定し、たとえば図の薄いグレーで塗った部分などの面積を求める必要があります。
数学的にいえば確率分布の曲線(確率密度曲線)を一定範囲で積分する、ということになります。
さて、以上のことを前提として、正規分布のさらに特徴的な点をいくつか挙げると、まず左右対称の確率分布になっている点が挙げられます。そうすると確率分布のちょうど真ん中のところが平均値(=期待値)となるのですが、各値の平均からのずれは、右方向にも左方向にも同じような割合で発生することになります。
次に、確率の大きさは、真ん中の平均のところで最も高くなっていて、そこから外れた値を取る確率は、その外れ方が大きくなるに従ってどんどん小さくなっていきます。その結果、確率密度曲線は山のような形になります。山のような形と書きましたが、正規分布の確率密度曲線は一般に釣り鐘型曲線(ベルカーブ)と呼ばれています。確率分布の両端の部分は、期待値から大きく外れた値が出現する確率を表すところですが、山の裾というイメージで“裾”と呼ばれます。英語では尻尾という意味の“テール”です。
また正規分布は、その研究を行なった数学者カール・フリードリッヒ・ガウスにちなんでガウス分布と呼ばれることもあります。
正規分布の便利な点は、正規分布に従って変動する確率変数を複数足し合わせた集合体の合計値や平均値も、やはり正規分布に従うという点です。たとえば、各銘柄の株価変動率が正規分布に従うならば、多数の銘柄を組み合わせた株式ポートフォリオの価値変動もまた正規分布に従うことになります。
複数を組み合わせても分布の性質が変わらないので、複数の変数を同時に扱う場合にも正規分布の仮定は大変便利なものになります。

※画像をクリックするとAmazonに飛びます。
- 28.2%の幻想と10.4%の現実、株式投資における期待リターンの捉え方
- ボラティリティとは何か? 期待リターンの裏に潜むもう1つの真実
- なぜ確率は「山の形」になるのか? 正規分布と中心極限定理
- ひとつのかごに卵を入れない、分散投資の知恵
- 株価はなぜ動く? 市場モデルで解き明かす「リスク」の正体
- 「VaR」が金融を変えた! リスク管理の常識を覆した革命とは
- 「過去は未来を保証しない」ブラック・スワンに備える思考法
