100人の村にビル・ゲイツが引っ越してきたら?
平均値が実感とかけ離れているのはなぜなのでしょうか。
たとえば、一般的な収入で暮らす100人の村人が住む地域に、ビル・ゲイツが引っ越してきたとしましょう。すると、その地域の平均年収は突然何億円にも跳ね上がります。平均値は極端な値に弱く、一番上の値が他とかけ離れていると、そこに引きずられて平均値が劇的に上がってしまうのです。つまり、総収入を村人の数で割って年収全体を均ならしても、極端な値が底上げした値に騙されるだけなのです。とくに、富裕層の収入は株式や不動産投資といった資産所得が大きなウエイトを占めるので、株式市場の変動に敏感に反応してしまいます。
一方で、中央値はデータを下や上から順に並べたとき、真ん中に来る値を表わしています。だからこそ、一般的な国民が手にする所得の感覚に近いと言えるのです。
そもそも、こうした誤解が生まれる背景には、世の中のデータのバラつきはすべて左右対称であり、平均値に一番大きな山がくるという思い込みがあるのではないでしょうか。こうした左右対称の図を正規分布と言いますが、所得を見てわかるとおり、現実にはもっとバラつきがあります。ちなみに、こうした左や右に傾いている図をワイブル分布と呼びます。
データのバラつきで集団の特徴がわかる
では、平均や正規分布はどんなときに使うのでしょうか。それは、各データのバラつき具合を知りたいときです(図2)。
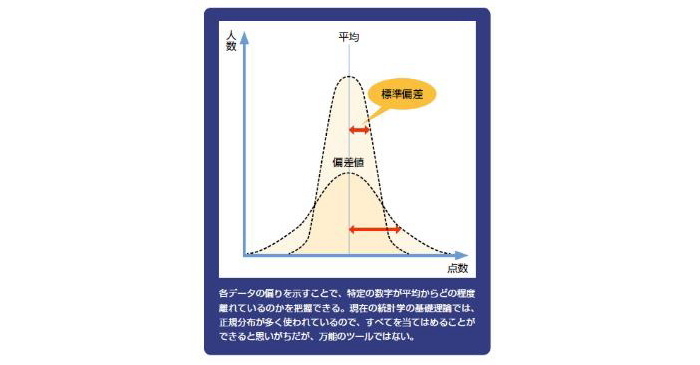
平均値を真ん中とし、各データがそこからどれだけ離れているかを示すことで、集団全体の特徴を表わす指標になり得るのです。
たとえば、学業における偏差値がわかりやすいでしょう。私の大学では、入学後すぐに生徒全員に数学のテストを受けてもらいます。すると、年度によって数値が一カ所に固まっているときもあれば、激しく散らばっているときもあります。このデータのバラつきの大きさが、標準偏差と呼ばれるものです。標準偏差が小さいと平均値付近の山は高くなり、大きいと山は低くなります。つまり、前者は突出して優秀な生徒はいないものの粒ぞろいの生徒が集まっている。後者は、できない人も多いが、そのぶん突出して優秀な生徒も多いという事実がわかるのです。このように、データからさまざまな特徴を読み解くことができます。
これだけわかれば、データを見て適切な判断を下せる確率は上がるはず。少なくとも、真偽不明のデータに騙されることは減るでしょうし、信頼できるデータも見つけやすくなるでしょう。ぜひ、ビジネスシーンで統計の知識を役立ててください。
神永正博(かみなが・まさひろ)東北学院大学工学部教授
1967年、東京都生まれ。京都大学大学院理学研究科数学専攻博士課程中退。博士(理学/大阪大学)。日立製作所中央研究所研究員などを経て現職。専門は暗号理論、数理物理。2010年度、数理科学研究所客員研究員として南インドに滞在。『未来思考』(朝日新聞出版)『ウソを見破る統計学』(講談社ブルーバックス)『不透明な時代を見抜く「統計思考力」』(日経ビジネス人文庫)など、著書多数。《取材構成:THE21編集部》(『THE21オンライン』2018年7月号より)
【関連記事 THE21オンラインより】
・数字が苦手でも大丈夫! ゼロから始める「財務3表」
・仕事の成果に直結する「2つの数学的思考力」とは?
・孫正義社長に叩き込まれた「数値化」仕事術とは?
・40代からでも取っておきたい「資格」
・世の中に出回る「数字」のウラを読み解け!