はじめに

最近、個人や企業を対象としたアンケート調査やパネルデータ、そしてビックデータと呼ばれる大規模のデータ等が蓄積されることにより、統計データを用いた実証分析(以下、統計分析)が多く行われている。過去と比べると、SPSS、Stata、Eviews、R等のような統計パッケージの普及により、統計分析がやりすくなったものの、依然として統計分析は難しい、手を出しづらいと思う人も少なくないだろう。統計分析の初心者にとって、数式を展開することや方程式の解を計算することは大変な作業であり、難解なものであるものの、よく使われる統計分析方法の基本概念さえ理解すれば、複雑な数式を使わなくてもより楽しく統計分析ができると筆者は確信する。そこで、本稿では、統計分析で最もよく使われているいくつかの分析方法を紹介する。これにより、統計分析に対する理解を深めてもらえたら幸いである。
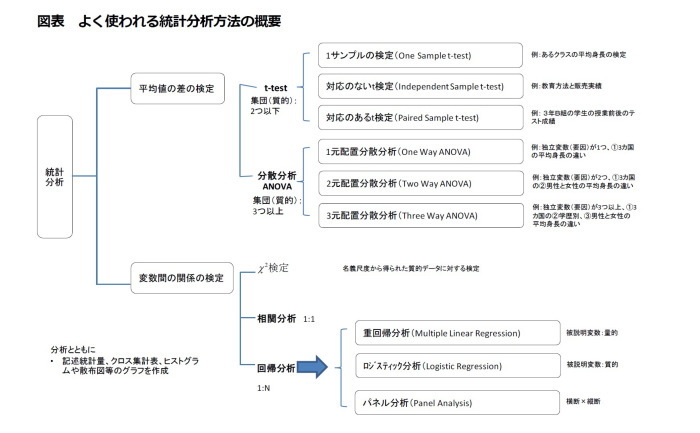
統計分析は大きく「差の検定」と「関係の検定」に区分
統計分析は大きく「差の検定」と「関係の検定」に区分することができる。差の検定は、平均値の差を検定する作業であり、集団が二つ以下である場合にはt-testにより、集団が三つ以上である場合には分散分析(ANOVA)により検定を行う。
一方、「関係の検定」はAという変数がBという変数に与える影響(関係)を分析する方法であり、(カイ二乗)検定(Chi-squared Test)、相関分析(Correlation Analysis)、回帰分析(Linear Regression)、ロジスティック分析(Logistic Regression)、パネル分析(Panel Analysis)などがよく使われている。
●平均値の差の検定
(1) t-test
t-test は、2つ以下の集団の平均の差を検定する方法であり、1)1サンプルの検定、2)対応のないt検定、3)対応のあるt 検定が代表的である。それぞれの例を以下に示す。
1) 1サンプルの検定
例)中学校1年生の平均身長が150Cmであるかどうかを検定する。
2) 対応のないt 検定
例) ある会社の男性と女性の賃金に差があるかどうかを検定する。
3) 対応のあるt 検定
例)授業前と授業後のテスト点数に差があるかどうかを検定する。
(2) 分散分析(ANOVA)
一方、分散分析は3つ以上の集団の平均の差を検定する方法であり、一般的には1)一元配置の分散分析、2)二元配置の分散分析、3)三元配置の分散分析がよく使われている。
1) 一元配置の分散分析
説明変数(要因)が1つ
例:3カ国の平均身長の違い
2) 二元配置の分散分析
説明変数(要因)が2つ
例:3カ国×男性と女性の平均身長の違い
3) 三元配置の分散分析
説明変数(要因)が3つ以上
例:3カ国×学歴別×男性と女性の平均身長の違い
●変数間の関係の検定
(1) (カイ二乗)検定
名義尺度(1)から得られた質的データに対する検定で、標本で得られた結果で母集団を推測できるかどうかを判断する方法である。具体的には期待度数(期待値・理論値)を求め、その期待度数から観測度数(測定された値)がどの程度の割合でずれているか(観測度数と期待度数の差=残差)を検定する。
-----------------------------------
(1)単に区別するために用いられている尺度。例えば、血液型のA型、B型、O型、AB型をそれぞれ1、2、3、4という数値に対応させたもの。平均、分散、標準偏差を求めても意味がない。
(2) 相関分析
散布図や相関係数をもとにして、2変数の関係を調べる統計解析の手法である。相関係数とは、 簡単にいうと2つの変数がどのような関係にあるのかを数値で表したものであり、相関係数は-1から+1の間の値をとる。一般的に相関係数はrで表記され、得られた相関係数は次のように解釈する。
・r=0のとき、2つの変数には関連性がない
・rが1 に近いときは2つの確率変数には正の相関がある
・rが-1 に近いときは2つの確率変数には負の相関がある
(3) 重回帰分析(線形回帰分析)
統計的分析方法の中で最も使われているのが回帰分析である。回帰分析を簡単に言うと、ある変数の値で、他の変数の値を予測し、両者の関連性を確認する分析方法だと言える。一般的には予測される変数を被説明変数(従属変数、目的変数とも呼ぶ)と呼び、予測のために使われる変数を説明変数(説明変数)と呼ぶ。また、被説明変数を予測する際に使われる説明変数が一つであると単回帰分析(simple regression model)であり、説明変数が二つ以上であると重回帰分析(multiple regression model)である。相関分析との大きな違いは相関分析が変数と変数の間の「1:1」の関係を分析することに対して、回帰分析は一つの被説明変数と多数の説明変数の関係、つまり「1:N」の関係を分析しているところだと言える。
(4) ロジスティック分析(非線形回帰分析)
一般的な回帰モデルは、説明変数と被説明変数の間の線形関係を仮定し、分析を行う。しかしながら社会のすべての現象が線形的な関係ではないので、非線形的な関係に対する分析も必要である。例えば所得がいくらぐらいである時、家を所有するのか、給料がどのぐらいある時、車を買うのか、年収がどのぐらいである時、結婚をするのかなど説明変数は量的データあるものの、被説明変数は「家を所有している、家を所有していない」などの質的データになっている場合がある。従って、被説明変数が質的変数である場合には重回帰分析(線形回帰分析)ではなく、ロジスティック分析(非線形回帰分析)を行う必要がある。つまり、ロジスティック回帰分析は質的変数である被説明変数の確率を予測する方法である。例えば、家を所有している場合を1、家を所有していない場合を0とする2値しかとりえない値を被説明変数の実績値として用い、説明変数を用いてその発生確率を予測することができる。
(5) パネル分析
パネル分析は、パネルデータを用いた分析方法である。パネルデータとは個人や企業等の複数の経済主体の情報を時系列で追跡したデータである。パネルデータを通常の回帰分析(最小二乗法)で推定した場合、推定値にバイアスが発生する恐れがある。つまり、通常の最小二乗法では企業や個人の持っている固有効果を誤差項に含めて推定を行っているが、その結果、固有効果により誤差項に自己相関が発生したり、誤差項が説明変数と相関するために、BLUE(Best Linear Unbiased Estimator、最良線形不偏推定量)を得るための誤差項の仮定が満たされなくなるケースが多い。そこで、パネル分析をすることにより、個体の観察されない固有効果がコントロールできるので、バイアスのある推定値を得るリスクを減らすことができるのである。また、それ以外のパネル分析のメリットとしては、個体のダイナミックな動きを測定することができる、サンプル数が増える、多重共線性(muiti-collinearity)の問題が緩和されることなどが挙げられる。
結びに代えて
本稿では最も一般的に使われている統計分析方法の概要を簡単に紹介した。本稿の内容は統計分析に対する理解を深めるのに貢献することを目的に書かれている。より多くの人が統計分析に対する苦手意識を乗り越え、より楽しく統計分析を活用することを願うところである。次回の「統計分析を理解しよう - ロジスティック分析のすべて-」も期待していただきたい。
金 明中(きむ みょんじゅん)
ニッセイ基礎研究所 生活研究部 准主任研究員・ヘルスケアリサーチセンター・ジェロントロジー推進室兼任
【関連記事 ニッセイ基礎研究所より】
・回帰分析を理解しよう!-回帰分析の由来と概念、そして分析結果の評価について-
・対数(自然対数)を理解しよう!-対数の定義と分析結果の解釈について-
・回帰分析の落とし穴-分析結果は、推論の正しさを裏付けているか?




