

「100万円が10年間で200万円になる投資」と「100万円を年率8%で10年間運用する投資」、どちらがいい投資といえるでしょうか。一見すると、2倍に増えているので前者の方がトクなようですが、実は後者の方が10年後の資産が215万円を超えるためトクだといえます。資産運用を上手に行うには、利益を正確に計算できなければなりません。この記事ではお金の価値が「時間」によってどのように変わるのか、その仕組みを解説します。
お金が増えても「いい投資」とは限らない
鈴木さん(60)は20年前の2003年4月に相続で3,000万円を手にしたので、運用方法をお金の専門家に相談しました。専門家は株式での運用を推奨し、鈴木さんは3,000万円すべてを勧められた国内株式に分散投資しました。結果、2023年3月時点では資産が5,000万円に増えました。
また、鈴木さんはこれまで毎年30万円ずつ貯蓄をしていたのですが、2003年以降はそれらも投資にまわすことを勧められました。米国株式をいくつか紹介されたので、毎月30万円を米国株に投資し始めました。その結果、元本600万円が800万円になりました。
さて、みなさんは鈴木さん同様、この「お金の専門家」に資産運用の相談をしますか?
鈴木さんは資産を大きく増やしているように見えますね。しかし、年率で換算すると相続で得た3,000万円は2.59%、積立金は2.93%のリターンにしかなっていないのです。
2003年から2023年の20年間、国内の代表的な株価指数であるTOPIXは平均4.81%、米国の代表的な株価指数であるS&P500は年利8.21%のリターンでした(いずれも2003年4月1日〜2023年3月31日まで)。もし鈴木さんが同程度のリスク特性を持つ株式市場の平均的なリターンを得ていたとすると、相続で得たお金は7,677万円、積立金は1,405万円になっていたはずです。
つまり、鈴木さんは(他によい選択肢があったという意味で)必ずしも「いい投資」をしたとはいえないのです。このように、お金が増えているからといって「いい投資」とは限りません。また、不況下でお金が減ったとしても、損失を最小現に抑えることができているなら、投資としては決して悪いとはいえないのです。
お金の時間的価値、その基本的な原理
「複利」という言葉を知っていても、その効果を正しく理解している人は多くありません。鈴木さんの例のように、ここ20年の国内株式の平均リターン4.8%を大きく下回る年利2.59%という運用成績でも、20年の複利を利用すると「3,000万円→5,000万円」と非常にいい投資に見えてしまいます。
投資の良し悪しを判断するには、「複利」と「投資期間」の2つのポイントを考慮する必要があります。
複利とは
複利では、投資した元本に利子がつく上に、利子にも利子がつきます。対して、投資元本にだけ利子がつくことを単利といいます。複利は単利に比べ、投資元本を大きく増やす効果があります。たとえば、100万円に金利5%で5年間、複利がつくとどうなるかを見てみましょう。
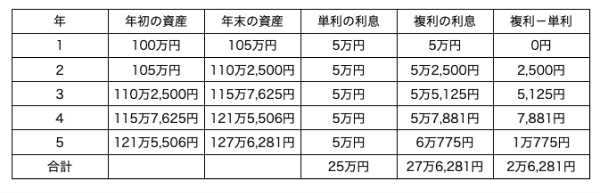
5年後の利息は複利が単利に比べ2万6,281円も多くなっています。これは単利の利息の合計額の1割を超える額です。
30年後の比較を見ると、複利の利息が単利の場合と比べてどれだけいいかがわかるのではないでしょうか。
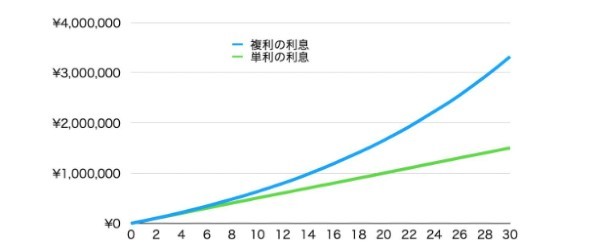
ここからは、複利と投資期間を考慮し、さまざまなお金の価値を表計算ソフト「エクセル」を用いて計算します。ぜひ実際に計算してみてください。
現在価値(Present Value)
現在価値とは、将来のお金の予想額(=将来価値)を掲示された時、それが現在ではどの程度の金額になるのかを表します。この現在価値は、将来価値を利率で割り戻すことで求められます。つまり、複利の逆を行うわけです。長い年月を考えると現在価値は将来価値に比べ、非常に少なくなります。
(例)年利が5%の場合、10年後の30万円の現在価値はいくらでしょうか?
エクセルで現在価値を求めるには、PV関数を使います。PV関数には5つの引数があり、PV(利率、期間、定期支払額、将来価値、支払期日)となります。「利率」「期間」「将来価値」はそれぞれ対応する値を入力します。「定期支払金」は定期金を扱うときに使うので、今は0を入力します。「支払期日」の入力は任意なので、ここでは入力しません。
最後にPVの前にマイナス符号をつけます。現在価値と将来価値は支払いと受け取りが逆になるため、どちらかにマイナスをつけることを忘れないようにしましょう。
- B2:B4の範囲にデータを入力
- セルB6に =-PV(B3,B4,0,B2)
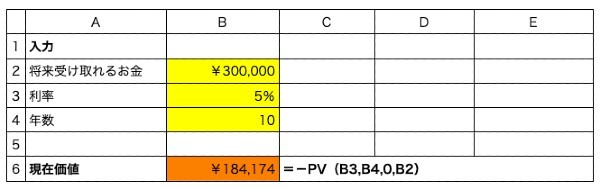
年利5%での運用が期待できるのであれば、10年後の30万円は現時点では18万4,174円の価値しかないことになります。
将来価値(Future Value)
将来価値とは、ある期間の終了後に得られることが予想される金額のことを指します。
(例)100万円を年利7%のリターンが期待できる先進国株式投資信託に投資すると、10年後にいくらになっているでしょうか。
エクセルで将来価値を求めるにはFV関数を使います。FV関数はFV(利率、期間、定期支払額、現在価値、支払期日)を入力します。PV関数とほとんど同じ引数ですが、4つ目が「現在価値」に変わります。
- B2:B4の範囲にデータを入力
- セルB6に =-FV(B3,B4,0,B2)
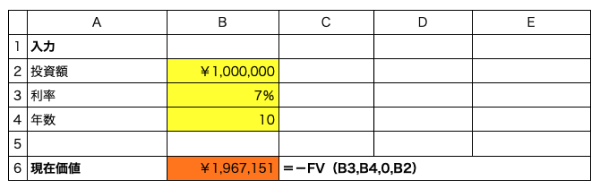
100万円を7%で運用すると、10年後には196万7,151円と倍近くに増えます。
金利(Rate)
金利や運用利率を計算したいときは、エクセルのRATE関数を使います。
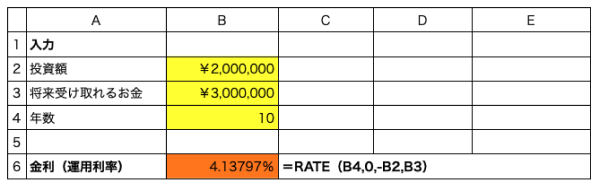
(例)あるファンドマネージャーは、10年間で200万円を300万円に増やしたといいます。年何パーセントで運用したことになるでしょうか。
RATE関数の引数はRATE(期間、定期支払額、現在価値、将来価値、支払期日、推定値)となります。「推定値」以外はすでに紹介していますが、推定値には正しいと思われる予想の数値を入力することになっており、入力しなくても構いません。
- B2:B4の範囲にデータを入力
- セルB6に =RATE(B4,0,-B2,B3)
定期積立金の将来価値
最後に、定期的に積み立てたお金が将来どのぐらいの金額になるかを計算してみましょう。
(例)子どもが生まれたので、毎年30万円ずつ投資に回すことにしました。運用率は3%を見込んでいます。18年後にはいくらになっているでしょうか。
求めるのは将来価値なので、FV関数「FV(利率、期間、定期支払額、現在価値、支払期日)」を使用します。ただし、この場合は開始時期のお金(現在価値)は0で、定期支払金が30万円になります。
- B2:B4の範囲にデータを入力
- セルB6に =-FV(B3,B4,B2,0)
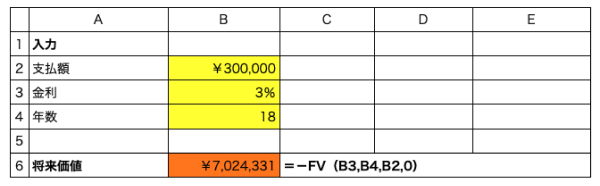
年間30万円は1カ月にすると2万5,000円です。この積み立てを続けると18年後には700万円以上になります。たとえば、教育資金などは子どもが生まれた時点から始めることで、複利の力を生かして無理なく準備することができます。
インフレを考慮したリターン
ここまでは、お金の価値が時間によってどう変わるのかをご紹介しました。これが理解できると、今日の100万円と5年後の120万円のどちらの価値が高いかが比較できますし、異なる基準で提示された投資先を選ぶときにも正しい選択をすることができるようになります。
お金の時間的価値を考えるにあたってもう1つ無視できないのが、インフレーション(以下インフレ)の影響です。実際、2022年は全体的に物の値上げが続きました。スーパーで買い物をしていて、物価が上がったことを実感した人が多いのではないでしょうか。
(物価が上昇する)インフレが起こると、投資で得られた利益が目減りすることがあります。インフレ調整をした資産のリターンを「実質リターン」といいます。「実質リターン」に対して、実際に受け取る金額に基づく資産のリターンを「名目リターン」といいます。みなさんがよく目にするのは「名目リターン」の方です。
実質リターンは次の式で計算できます。
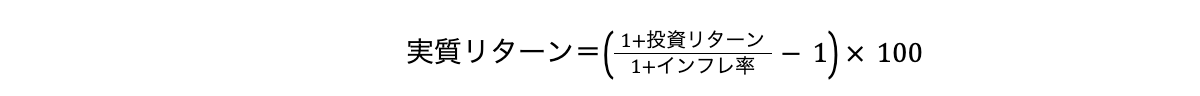
たとえば、2022年に投資で3%の利益が出たとします(名目リターン3%)。しかし、IMF(国際通貨基金)の発表によると、2022年の日本のインフレ率は1.989%程度と推定されています。この推定が正しいとすると、名目リターン3%の2022年度の実質リターンは、
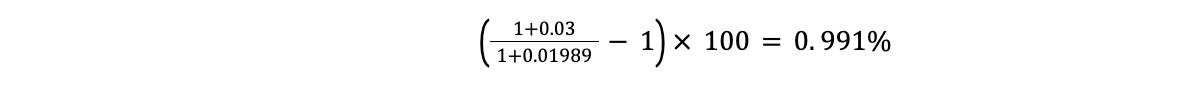
となり、実質は1%弱しか資産が増えていないことになります。
当然インフレ率より名目リターンが低ければ、資産は目減りしています。たとえばすべての資産を0.001%の普通預金で保有していると、実質リターンは、
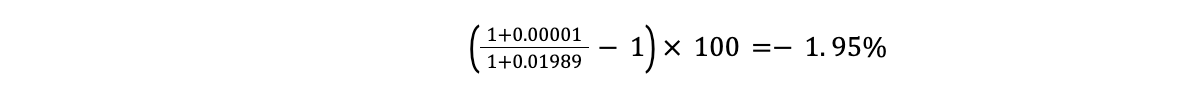
となります。これは実質的に-2%で運用しているということです。
もちろん、今後もインフレ率がこのようなペースで続くとは限りません。しかし、今後のインフレ率に見合うリターンを得なければ、今の資産で購入できる物の数は減っていきます。実際に資産運用を考えるときは、インフレの影響を考慮に入れることでより実態に近いプランを立てることができます。
さらに情報を知りたい方へ
キャッシュフローの最大化を図るには節税はもちろん、さらに効果的な資産運用サービスを知っておく必要があります。
詳しい情報をご希望の方は、株式会社ZUU 富裕層向け金融サービス専用フォームからのお問い合わせをおすすめします。
資金調達の方法に始まり、運用から、償却に至るまでのキャッシュフロー全般の情報を、 金融機関65社との接点を持つZUUグループなら「中立的」な立場で紹介可能です。
ZUUグループでは、これまでに保有資産額10億円〜100億円超の方々に至るまで、 不動産、外国債権、ブリッジローンといった幅広い金融サービスをご提案してきました。
まずは以下のフォームで回答してみましょう(所要時間1分)。
