本記事は、NightWalker氏の著書『最強のインデックス投資』(ぱる出版)の中から一部を抜粋・編集しています。

アセットアロケーション(資産配分)は「取れるリスク」から考える
投資の世界では、資産配分(アセットアロケーション)が、投資のリターンとリスクをほぼ決めると言われています。資産配分を決める場合、つい欲しいリターンを考えて資産配分を考えてしまいがちなのですが、リターンを先に考えると往々にしてリスクを取り過ぎてしまい、しばしば長期投資の妨げになってしまいがちです。
ですので、私は、リスクを先に考えて資産配分を決める方法をオススメしています。私の経験則からも、自分自身にとって適切なリスクを取れるかどうかが、長期投資の成功率のほとんどを決めると考えます。
「自分自身にとって適切なリスクを取り続ける」
リスクは取り過ぎても少な過ぎてもダメなのです。取り過ぎれば運用を失い、取らなさ過ぎるとリターンを失います。
【超重要】リスク資産と無リスク資産の比率を考える
具体的なリスクコントロールの要となるのが、リスク資産と無リスク資産の比率です。ついリスク資産の中身の配分をいろいろ考えてしまいがちですが、重要なのは無リスク資産の比率です。リスク資産を熱湯とするなら、無リスク資産は水。自分にとっての適温に薄めることが大切なのです。
無リスク資産とは、元本割れのリスクがほとんどない資産のことで、短期債券(MRFなど)、預金、個人向け国債などがあります。無リスク資産は、インフレ要因を除けば値下がりすることがありません。このため、心理的な安心感につながります。
もうひとつの重要な利点は流動性です。
「いざというとき」に、さっと動かせるお金というのは強いということを「いざというとき」が来る前、できれば平穏時に無リスク資産の比率を考えておいた方が良いでしょう。
インデックス投資の土台となった現代ポートフォリオ理論
ここで、インデックスファンドとは何か、少し理論的な背景を説明しておこうと思います。インデックス投資は、ノーベル賞を取ったハリー・マーコウィッツさん(1927〜2023)の現代ポートフォリオ理論(Modern portfolio theory, MPT)という理論が基礎となっています。最新のフィンテックやロボアドバイザーなどもこの理論が使われています。
現代ポートフォリオ理論によると合理的な投資家が取るべき行動は、以下のような単純なものとなります。
「たったひとつしかない最適に分散されたリスク資産の組合せを、無リスク資産と組合せて保有する」
「たったひとつしかない最適に分散されたリスク資産の組合せ」とは、「市場ポートフォリオ」。これは、市場の縮小コピー、市場そのものに連動する指数です。市場にある全銘柄をその時価総額の比率で投資することで実現できます。すなわち、時価総額分散型のインデックスファンドのことなのです。
そして、21世紀の日本では、投資範囲を全世界に拡げた「世界市場ポートフォリオ」に連動するインデックスファンド=オールカントリーを買うことができます。いい時代になりました。
現代ポートフォリオ理論では、リスク資産(たとえばある会社の株)を次の3つの要素でモデル化しています。
- (1)リスク資産の標準偏差
(2)リスク資産の期待リターン
(3)リスク資産同士の相関係数
これら3つの要素の中に、インデックス投資家がチェックすべき重要なチェックポイントが含まれています。資産形成のためにインデックス投資をする人は、この3つを押さえておけば充分です。
ポイント(1) 標準偏差
現代ポートフォリオ理論で、株価変動がどんな風にばらついているかを示すのが、数学でおなじみの正規分布の図です(図4-④)。
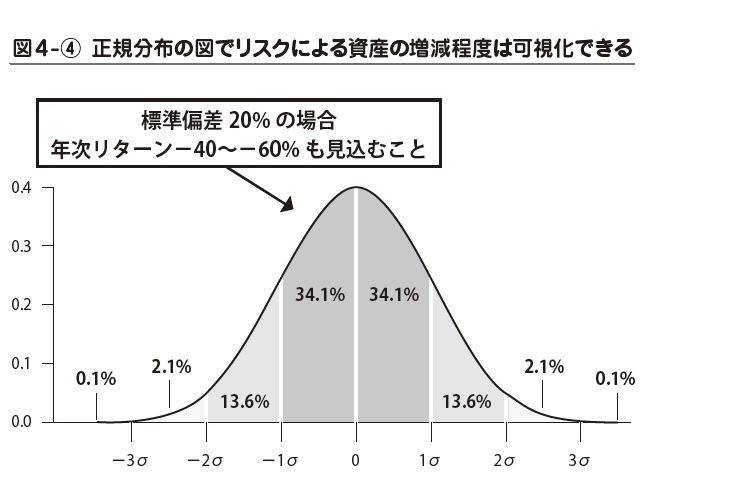
株価の場合にどう見るかというと、横軸がリターン。縦軸は発生頻度です。中央が、期待リターンを示していて、σシグマというのが、標準偏差、すなわちリターンのばらつきを示します。
情報共有が発達した現代なら市場に参加している人は効率的に行動するに違いない。とするなら、株価もブラウン運動のようにランダムに動くはずだ……と仮定することで、株価の動きを正規分布するサイコロのモデルにしちゃったのです。すごい発想です。
この考え方は、私たちが一時的にせよリスクによって、どの程度お金が減ることを覚悟しておかなければいけないのかを判断する材料として使えます。たとえば、株の標準偏差は年次リターン20%〜30%分くらいと言われています。標準偏差が20%だった場合を考えてみましょう。この場合、図から読み取れるのは、マイナスリターンが、20%以内に収まる確率=34.1%マイナスリターンが、40%以内に収まる確率=47.7%マイナスリターンが、60%以内に収まる確率=49.8%
年次リターンがマイナス40〜%になる可能性を見込んでおけば、確率的には、ほとんどのケースをカバーすることができることがわかります。リスク資産が一時的に半分になっても大丈夫か? という資産設計のためのアイデアがあります。それは、株価の変動を確率で表現するという、こんな理論的背景があるのです。
ポイント(2) 期待リターンに期待しない
投資家が、もっとも気になるのが、期待リターンです。期待リターンは、正確にはわかりません。
理由は2つあります。第一に、長期の期待リターンを計算するには、過去のデータが不足しています。たとえば、日経平均株価の20年間の期待リターンの平均を知りたいとします。ところが、日経平均株価は、1950年が始まりで、たかだか、70年とちょっとの歴史しかありません。
たとえば、戦後復興期のハイパーインフレ時代が、半分くらいの影響力がある一方で、バブル崩壊という金融史に残りそうな長期低迷期が半分くらいを占めています。特殊な状況が大半を占めるデータを平均した結果で、これからを占うのは、少々、気が引けます。
第2に、長期と言っても人間には寿命があるということです。100年間、バイアンドホールドするのは、不可能です。もちろん、相続税や政治的異常事態による資産没収がなく王朝システムを構築できるとするなら、先祖代々、大きな財産が築けたはずですが、庶民には非現実的です。
期待リターンにしても、20年とか、30年単位で考えるのが、一人の人間の限界となります。しかし、実際の過去の相場を見ていると、20年くらい堅調な期間が続いたかと思うと、20年くらい停滞期が続いたりすることは良くあります。どうなるかわからない将来のリターンを算段に入れてしまうのは、無理なところもあるのです。
つまり、期待リターンにあんまり期待してはいけないのです。
ただ、どのくらいか知りたいと思うのも人情です。
益利回りというのですが、市場がどの程度の利益を企業に期待しているか、ということからだいたいの株式のリターンを求めることができます。現在の株価が、その会社(インデックスの場合、市場)の何年分の利益に相当するかを数値化したPERという指標があります。そして、PERの逆数を取ると、益利回りを求めることができます。PERは16倍程度、つまり株式の時価総額を回収するのに16年かかる、というのがこれまでの市場の平均だと言われています。そこから判断すると、1÷16で、6%ぐらいが、株式の期待リターンの妥当な値と考えられます。
ポイント(3) 分散効果を高める組合せ
現代ポートフォリオ理論では、分散効果を高めるには、相関関係があまりない資産を組み合わせると良い、ということが示されています。
異なるリスク資産を組合せるとき「リスク(標準偏差)」、「期待リターン」と並んで「相関係数」というパラメータを使います。相関係数とは、−1〜+1の間を取る数値で、まったく同じ動きをするときは、「+1」、全く逆の動きをするときには「−1」になります。
そして、相関関係が小さいほど、分散効果が高くなります。つまり、リスクが減ります。
全く同じ「リスク(標準偏差)」、「期待リターン」を持つ、資産Aと資産Bがあって、相関係数が「+1」の資産同士であれば、期待リターンもリスクも全く変わりません。分散効果が全くないのです。
一方、同じ条件でも相関係数が、全く逆の動きをする「−1」のときは、期待リターンは全く変わらずリスクだけがゼロになります。たとえばそのような組合せがあった場合、無リスクで期待リターンだけが残るという理想的なポートフォリオができます(残念ながら、そのような組合せは、現実には存在していません)。

自身が運用中のポートフォリオは、目下、全世界株式一本に集約中。無リスク資産を50%にしたリスク抑えめのカウチポテト運用。著書は『世界一ラクなお金の増やし方 #インデックス投資はじめました』(ぱる出版)。※画像をクリックするとAmazonに飛びます。
